Raster Calculations
Last updated on 2024-10-15 | Edit this page
Estimated time: 60 minutes
Overview
Questions
- How do I subtract one raster from another and extract pixel values for defined locations?
Objectives
- Perform a subtraction between two rasters using raster math.
- Perform a more efficient subtraction between two rasters using the
raster
lapp()function. - Export raster data as a GeoTIFF file.
Things You’ll Need To Complete This Episode
See the lesson homepage for detailed information about the software, data, and other prerequisites you will need to work through the examples in this episode.
We often want to combine values of and perform calculations on
rasters to create a new output raster. This episode covers how to
subtract one raster from another using basic raster math and the
lapp() function. It also covers how to extract pixel values
from a set of locations - for example a buffer region around plot
locations at a field site.
Raster Calculations in R
We often want to perform calculations on two or more rasters to create a new output raster. For example, if we are interested in mapping the heights of trees across an entire field site, we might want to calculate the difference between the Digital Surface Model (DSM, tops of trees) and the Digital Terrain Model (DTM, ground level). The resulting dataset is referred to as a Canopy Height Model (CHM) and represents the actual height of trees, buildings, etc. with the influence of ground elevation removed.

More Resources
- Check out more on LiDAR CHM, DTM and DSM in this NEON Data Skills overview tutorial: What is a CHM, DSM and DTM? About Gridded, Raster LiDAR Data.
Load the Data
For this episode, we will use the DTM and DSM from the NEON Harvard Forest Field site and San Joaquin Experimental Range, which we already have loaded from previous episodes.
Exercise
Use the describe() function to view information about
the DTM and DSM data files. Do the two rasters have the same or
different CRSs and resolutions? Do they both have defined minimum and
maximum values?
R
describe("data/NEON-DS-Airborne-Remote-Sensing/HARV/DTM/HARV_dtmCrop.tif")
OUTPUT
[1] "Driver: GTiff/GeoTIFF"
[2] "Files: data/NEON-DS-Airborne-Remote-Sensing/HARV/DTM/HARV_dtmCrop.tif"
[3] "Size is 1697, 1367"
[4] "Coordinate System is:"
[5] "PROJCRS[\"WGS 84 / UTM zone 18N\","
[6] " BASEGEOGCRS[\"WGS 84\","
[7] " DATUM[\"World Geodetic System 1984\","
[8] " ELLIPSOID[\"WGS 84\",6378137,298.257223563,"
[9] " LENGTHUNIT[\"metre\",1]]],"
[10] " PRIMEM[\"Greenwich\",0,"
[11] " ANGLEUNIT[\"degree\",0.0174532925199433]],"
[12] " ID[\"EPSG\",4326]],"
[13] " CONVERSION[\"UTM zone 18N\","
[14] " METHOD[\"Transverse Mercator\","
[15] " ID[\"EPSG\",9807]],"
[16] " PARAMETER[\"Latitude of natural origin\",0,"
[17] " ANGLEUNIT[\"degree\",0.0174532925199433],"
[18] " ID[\"EPSG\",8801]],"
[19] " PARAMETER[\"Longitude of natural origin\",-75,"
[20] " ANGLEUNIT[\"degree\",0.0174532925199433],"
[21] " ID[\"EPSG\",8802]],"
[22] " PARAMETER[\"Scale factor at natural origin\",0.9996,"
[23] " SCALEUNIT[\"unity\",1],"
[24] " ID[\"EPSG\",8805]],"
[25] " PARAMETER[\"False easting\",500000,"
[26] " LENGTHUNIT[\"metre\",1],"
[27] " ID[\"EPSG\",8806]],"
[28] " PARAMETER[\"False northing\",0,"
[29] " LENGTHUNIT[\"metre\",1],"
[30] " ID[\"EPSG\",8807]]],"
[31] " CS[Cartesian,2],"
[32] " AXIS[\"(E)\",east,"
[33] " ORDER[1],"
[34] " LENGTHUNIT[\"metre\",1]],"
[35] " AXIS[\"(N)\",north,"
[36] " ORDER[2],"
[37] " LENGTHUNIT[\"metre\",1]],"
[38] " USAGE["
[39] " SCOPE[\"Engineering survey, topographic mapping.\"],"
[40] " AREA[\"Between 78°W and 72°W, northern hemisphere between equator and 84°N, onshore and offshore. Bahamas. Canada - Nunavut; Ontario; Quebec. Colombia. Cuba. Ecuador. Greenland. Haiti. Jamica. Panama. Turks and Caicos Islands. United States (USA). Venezuela.\"],"
[41] " BBOX[0,-78,84,-72]],"
[42] " ID[\"EPSG\",32618]]"
[43] "Data axis to CRS axis mapping: 1,2"
[44] "Origin = (731453.000000000000000,4713838.000000000000000)"
[45] "Pixel Size = (1.000000000000000,-1.000000000000000)"
[46] "Metadata:"
[47] " AREA_OR_POINT=Area"
[48] "Image Structure Metadata:"
[49] " COMPRESSION=LZW"
[50] " INTERLEAVE=BAND"
[51] "Corner Coordinates:"
[52] "Upper Left ( 731453.000, 4713838.000) ( 72d10'52.71\"W, 42d32'32.18\"N)"
[53] "Lower Left ( 731453.000, 4712471.000) ( 72d10'54.71\"W, 42d31'47.92\"N)"
[54] "Upper Right ( 733150.000, 4713838.000) ( 72d 9'38.40\"W, 42d32'30.35\"N)"
[55] "Lower Right ( 733150.000, 4712471.000) ( 72d 9'40.41\"W, 42d31'46.08\"N)"
[56] "Center ( 732301.500, 4713154.500) ( 72d10'16.56\"W, 42d32' 9.13\"N)"
[57] "Band 1 Block=1697x1 Type=Float64, ColorInterp=Gray"
[58] " Min=304.560 Max=389.820 "
[59] " Minimum=304.560, Maximum=389.820, Mean=344.898, StdDev=15.861"
[60] " NoData Value=-9999"
[61] " Metadata:"
[62] " STATISTICS_MAXIMUM=389.81997680664"
[63] " STATISTICS_MEAN=344.8979433625"
[64] " STATISTICS_MINIMUM=304.55999755859"
[65] " STATISTICS_STDDEV=15.861471000978" R
describe("data/NEON-DS-Airborne-Remote-Sensing/HARV/DSM/HARV_dsmCrop.tif")
OUTPUT
[1] "Driver: GTiff/GeoTIFF"
[2] "Files: data/NEON-DS-Airborne-Remote-Sensing/HARV/DSM/HARV_dsmCrop.tif"
[3] "Size is 1697, 1367"
[4] "Coordinate System is:"
[5] "PROJCRS[\"WGS 84 / UTM zone 18N\","
[6] " BASEGEOGCRS[\"WGS 84\","
[7] " DATUM[\"World Geodetic System 1984\","
[8] " ELLIPSOID[\"WGS 84\",6378137,298.257223563,"
[9] " LENGTHUNIT[\"metre\",1]]],"
[10] " PRIMEM[\"Greenwich\",0,"
[11] " ANGLEUNIT[\"degree\",0.0174532925199433]],"
[12] " ID[\"EPSG\",4326]],"
[13] " CONVERSION[\"UTM zone 18N\","
[14] " METHOD[\"Transverse Mercator\","
[15] " ID[\"EPSG\",9807]],"
[16] " PARAMETER[\"Latitude of natural origin\",0,"
[17] " ANGLEUNIT[\"degree\",0.0174532925199433],"
[18] " ID[\"EPSG\",8801]],"
[19] " PARAMETER[\"Longitude of natural origin\",-75,"
[20] " ANGLEUNIT[\"degree\",0.0174532925199433],"
[21] " ID[\"EPSG\",8802]],"
[22] " PARAMETER[\"Scale factor at natural origin\",0.9996,"
[23] " SCALEUNIT[\"unity\",1],"
[24] " ID[\"EPSG\",8805]],"
[25] " PARAMETER[\"False easting\",500000,"
[26] " LENGTHUNIT[\"metre\",1],"
[27] " ID[\"EPSG\",8806]],"
[28] " PARAMETER[\"False northing\",0,"
[29] " LENGTHUNIT[\"metre\",1],"
[30] " ID[\"EPSG\",8807]]],"
[31] " CS[Cartesian,2],"
[32] " AXIS[\"(E)\",east,"
[33] " ORDER[1],"
[34] " LENGTHUNIT[\"metre\",1]],"
[35] " AXIS[\"(N)\",north,"
[36] " ORDER[2],"
[37] " LENGTHUNIT[\"metre\",1]],"
[38] " USAGE["
[39] " SCOPE[\"Engineering survey, topographic mapping.\"],"
[40] " AREA[\"Between 78°W and 72°W, northern hemisphere between equator and 84°N, onshore and offshore. Bahamas. Canada - Nunavut; Ontario; Quebec. Colombia. Cuba. Ecuador. Greenland. Haiti. Jamica. Panama. Turks and Caicos Islands. United States (USA). Venezuela.\"],"
[41] " BBOX[0,-78,84,-72]],"
[42] " ID[\"EPSG\",32618]]"
[43] "Data axis to CRS axis mapping: 1,2"
[44] "Origin = (731453.000000000000000,4713838.000000000000000)"
[45] "Pixel Size = (1.000000000000000,-1.000000000000000)"
[46] "Metadata:"
[47] " AREA_OR_POINT=Area"
[48] "Image Structure Metadata:"
[49] " COMPRESSION=LZW"
[50] " INTERLEAVE=BAND"
[51] "Corner Coordinates:"
[52] "Upper Left ( 731453.000, 4713838.000) ( 72d10'52.71\"W, 42d32'32.18\"N)"
[53] "Lower Left ( 731453.000, 4712471.000) ( 72d10'54.71\"W, 42d31'47.92\"N)"
[54] "Upper Right ( 733150.000, 4713838.000) ( 72d 9'38.40\"W, 42d32'30.35\"N)"
[55] "Lower Right ( 733150.000, 4712471.000) ( 72d 9'40.41\"W, 42d31'46.08\"N)"
[56] "Center ( 732301.500, 4713154.500) ( 72d10'16.56\"W, 42d32' 9.13\"N)"
[57] "Band 1 Block=1697x1 Type=Float64, ColorInterp=Gray"
[58] " Min=305.070 Max=416.070 "
[59] " Minimum=305.070, Maximum=416.070, Mean=359.853, StdDev=17.832"
[60] " NoData Value=-9999"
[61] " Metadata:"
[62] " STATISTICS_MAXIMUM=416.06997680664"
[63] " STATISTICS_MEAN=359.85311802914"
[64] " STATISTICS_MINIMUM=305.07000732422"
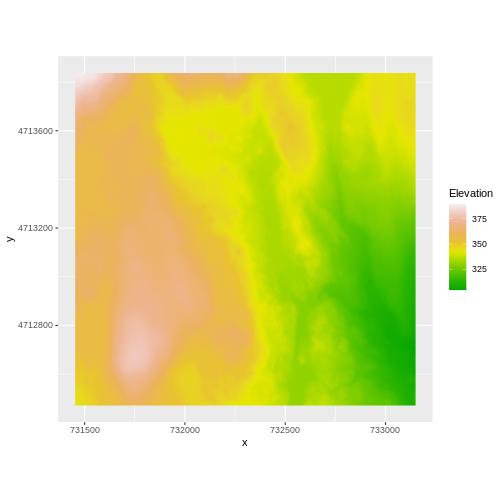
[65] " STATISTICS_STDDEV=17.83169335933" We’ve already loaded and worked with these two data files in earlier episodes. Let’s plot them each once more to remind ourselves what this data looks like. First we’ll plot the DTM elevation data:
R
ggplot() +
geom_raster(data = DTM_HARV_df ,
aes(x = x, y = y, fill = HARV_dtmCrop)) +
scale_fill_gradientn(name = "Elevation", colors = terrain.colors(10)) +
coord_quickmap()
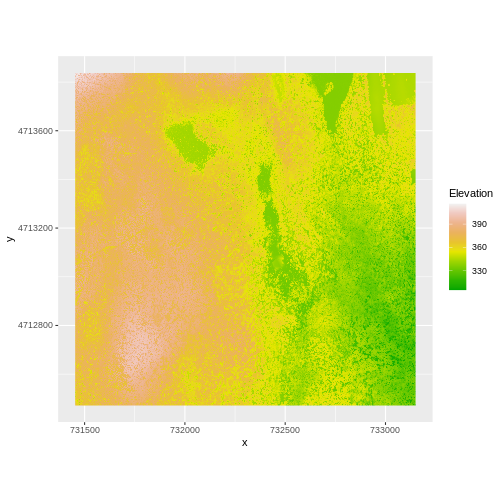
And then the DSM elevation data:
R
ggplot() +
geom_raster(data = DSM_HARV_df ,
aes(x = x, y = y, fill = HARV_dsmCrop)) +
scale_fill_gradientn(name = "Elevation", colors = terrain.colors(10)) +
coord_quickmap()
Two Ways to Perform Raster Calculations
We can calculate the difference between two rasters in two different ways:
- by directly subtracting the two rasters in R using raster math
or for more efficient processing - particularly if our rasters are large and/or the calculations we are performing are complex:
- using the
lapp()function.
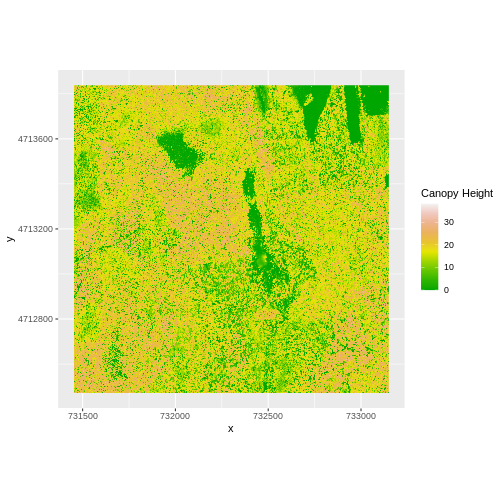
Raster Math & Canopy Height Models
We can perform raster calculations by subtracting (or adding, multiplying, etc) two rasters. In the geospatial world, we call this “raster math”.
Let’s subtract the DTM from the DSM to create a Canopy Height Model.
After subtracting, let’s create a dataframe so we can plot with
ggplot.
R
CHM_HARV <- DSM_HARV - DTM_HARV
CHM_HARV_df <- as.data.frame(CHM_HARV, xy = TRUE)
We can now plot the output CHM.
R
ggplot() +
geom_raster(data = CHM_HARV_df ,
aes(x = x, y = y, fill = HARV_dsmCrop)) +
scale_fill_gradientn(name = "Canopy Height", colors = terrain.colors(10)) +
coord_quickmap()
Let’s have a look at the distribution of values in our newly created Canopy Height Model (CHM).
R
ggplot(CHM_HARV_df) +
geom_histogram(aes(HARV_dsmCrop))
OUTPUT
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.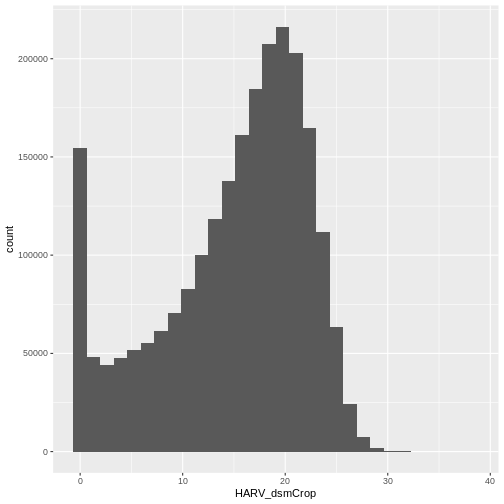
Notice that the range of values for the output CHM is between 0 and 30 meters. Does this make sense for trees in Harvard Forest?
Challenge: Explore CHM Raster Values
It’s often a good idea to explore the range of values in a raster dataset just like we might explore a dataset that we collected in the field.
- What is the min and maximum value for the Harvard Forest Canopy
Height Model (
CHM_HARV) that we just created? - What are two ways you can check this range of data for
CHM_HARV? - What is the distribution of all the pixel values in the CHM?
- Plot a histogram with 6 bins instead of the default and change the color of the histogram.
- Plot the
CHM_HARVraster using breaks that make sense for the data. Include an appropriate color palette for the data, plot title and no axes ticks / labels.
- There are missing values in our data, so we need to specify
na.rm = TRUE.
R
min(CHM_HARV_df$HARV_dsmCrop, na.rm = TRUE)
OUTPUT
[1] 0R
max(CHM_HARV_df$HARV_dsmCrop, na.rm = TRUE)
OUTPUT
[1] 38.16998- Possible ways include:
- Create a histogram
- Use the
min(),max(), andrange()functions. - Print the object and look at the
valuesattribute.
R
ggplot(CHM_HARV_df) +
geom_histogram(aes(HARV_dsmCrop))
OUTPUT
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.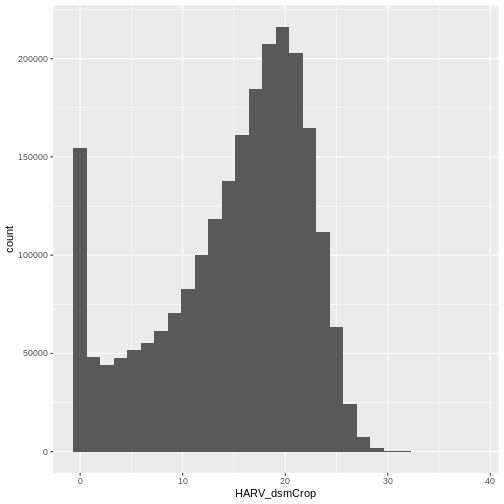
R
ggplot(CHM_HARV_df) +
geom_histogram(aes(HARV_dsmCrop), colour="black",
fill="darkgreen", bins = 6)

R
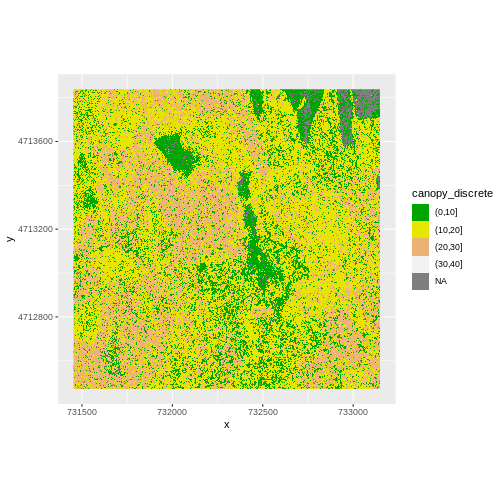
custom_bins <- c(0, 10, 20, 30, 40)
CHM_HARV_df <- CHM_HARV_df %>%
mutate(canopy_discrete = cut(HARV_dsmCrop,
breaks = custom_bins))
ggplot() +
geom_raster(data = CHM_HARV_df , aes(x = x, y = y,
fill = canopy_discrete)) +
scale_fill_manual(values = terrain.colors(4)) +
coord_quickmap()
Efficient Raster Calculations
Raster math, like we just did, is an appropriate approach to raster calculations if:
- The rasters we are using are small in size.
- The calculations we are performing are simple.
However, raster math is a less efficient approach as computation becomes more complex or as file sizes become large.
The lapp() function takes two or more rasters and
applies a function to them using efficient processing methods. The
syntax is
outputRaster <- lapp(x, fun=functionName)
In which raster can be either a SpatRaster or a SpatRasterDataset
which is an object that holds rasters. See help(sds).
Data Tip
To create a SpatRasterDataset, we call the function sds
which can take a list of raster objects (each one created by calling
rast).
Let’s perform the same subtraction calculation that we calculated
above using raster math, using the lapp() function.
Data Tip
A custom function consists of a defined set of commands performed on
a input object. Custom functions are particularly useful for tasks that
need to be repeated over and over in the code. A simplified syntax for
writing a custom function in R is:
function_name <- function(variable1, variable2) { WhatYouWantDone, WhatToReturn}
R
CHM_ov_HARV <- lapp(sds(list(DSM_HARV, DTM_HARV)),
fun = function(r1, r2) { return( r1 - r2) })
Next we need to convert our new object to a data frame for plotting
with ggplot.
R
CHM_ov_HARV_df <- as.data.frame(CHM_ov_HARV, xy = TRUE)
Now we can plot the CHM:
R
ggplot() +
geom_raster(data = CHM_ov_HARV_df,
aes(x = x, y = y, fill = HARV_dsmCrop)) +
scale_fill_gradientn(name = "Canopy Height", colors = terrain.colors(10)) +
coord_quickmap()
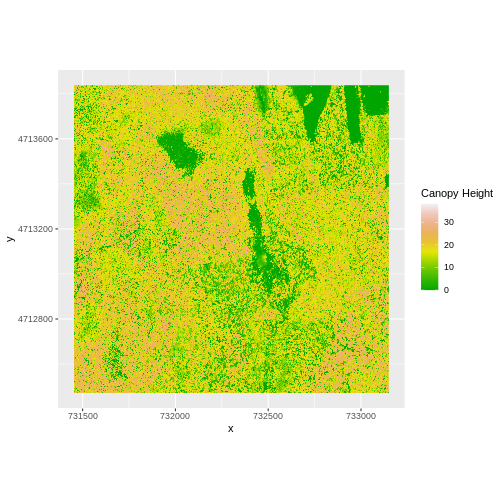
How do the plots of the CHM created with manual raster math and the
lapp() function compare?
Export a GeoTIFF
Now that we’ve created a new raster, let’s export the data as a
GeoTIFF file using the writeRaster() function.
When we write this raster object to a GeoTIFF file we’ll name it
CHM_HARV.tiff. This name allows us to quickly remember both
what the data contains (CHM data) and for where (HARVard Forest). The
writeRaster() function by default writes the output file to
your working directory unless you specify a full file path.
We will specify the output format (“GTiff”), the no data value
NAflag = -9999. We will also tell R to overwrite any data
that is already in a file of the same name.
R
writeRaster(CHM_ov_HARV, "CHM_HARV.tiff",
filetype="GTiff",
overwrite=TRUE,
NAflag=-9999)
writeRaster() Options
The function arguments that we used above include:
-
filetype: specify that the format will be
GTiffor GeoTIFF. - overwrite: If TRUE, R will overwrite any existing file with the same name in the specified directory. USE THIS SETTING WITH CAUTION!
-
NAflag: set the GeoTIFF tag for
NoDataValueto -9999, the National Ecological Observatory Network’s (NEON) standardNoDataValue.
Challenge: Explore the NEON San Joaquin Experimental Range Field Site
Data are often more interesting and powerful when we compare them across various locations. Let’s compare some data collected over Harvard Forest to data collected in Southern California. The NEON San Joaquin Experimental Range (SJER) field site located in Southern California has a very different ecosystem and climate than the NEON Harvard Forest Field Site in Massachusetts.
Import the SJER DSM and DTM raster files and create a Canopy Height
Model. Then compare the two sites. Be sure to name your R objects and
outputs carefully, as follows: objectType_SJER
(e.g. DSM_SJER). This will help you keep track of data from
different sites!
- You should have the DSM and DTM data for the SJER site already loaded from the Plot Raster Data in R episode.) Don’t forget to check the CRSs and units of the data.
- Create a CHM from the two raster layers and check to make sure the data are what you expect.
- Plot the CHM from SJER.
- Export the SJER CHM as a GeoTIFF.
- Compare the vegetation structure of the Harvard Forest and San Joaquin Experimental Range.
- Use the
lapp()function to subtract the two rasters & create the CHM.
R
CHM_ov_SJER <- lapp(sds(list(DSM_SJER, DTM_SJER)),
fun = function(r1, r2){ return(r1 - r2) })
Convert the output to a dataframe:
R
CHM_ov_SJER_df <- as.data.frame(CHM_ov_SJER, xy = TRUE)
Create a histogram to check that the data distribution makes sense:
R
ggplot(CHM_ov_SJER_df) +
geom_histogram(aes(SJER_dsmCrop))
OUTPUT
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.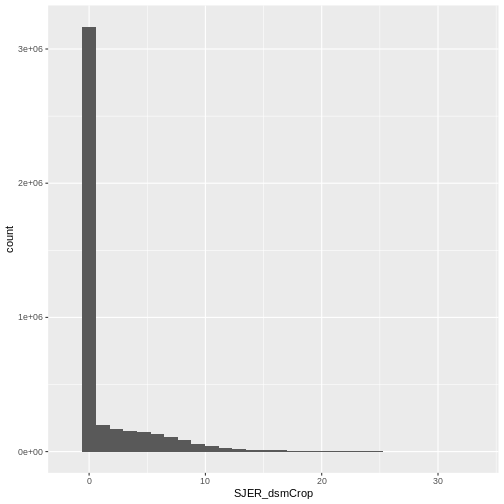
- Create a plot of the CHM:
R
ggplot() +
geom_raster(data = CHM_ov_SJER_df,
aes(x = x, y = y,
fill = SJER_dsmCrop)
) +
scale_fill_gradientn(name = "Canopy Height",
colors = terrain.colors(10)) +
coord_quickmap()

- Export the CHM object to a file:
R
writeRaster(CHM_ov_SJER, "chm_ov_SJER.tiff",
filetype = "GTiff",
overwrite = TRUE,
NAflag = -9999)
- Compare the SJER and HARV CHMs. Tree heights are much shorter in SJER. You can confirm this by looking at the histograms of the two CHMs.
R
ggplot(CHM_HARV_df) +
geom_histogram(aes(HARV_dsmCrop))
OUTPUT
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.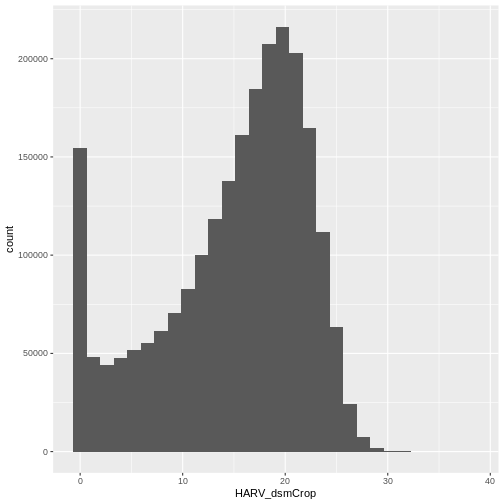
R
ggplot(CHM_ov_SJER_df) +
geom_histogram(aes(SJER_dsmCrop))
OUTPUT
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.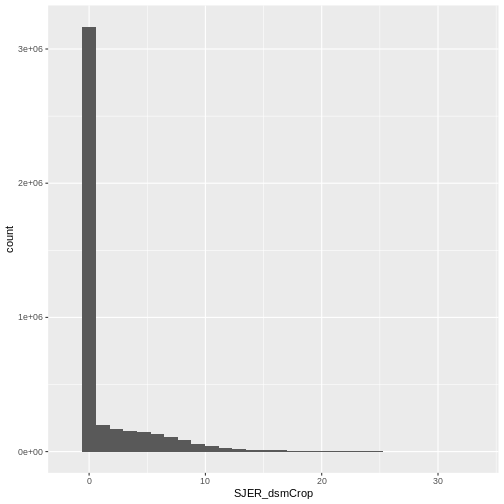
Key Points
- Rasters can be computed on using mathematical functions.
- The
lapp()function provides an efficient way to do raster math. - The
writeRaster()function can be used to write raster data to a file.
