Connected Component Analysis
Last updated on 2024-03-12 | Edit this page
Estimated time: 125 minutes
Overview
Questions
- How to extract separate objects from an image and describe these objects quantitatively.
Objectives
- Understand the term object in the context of images.
- Learn about pixel connectivity.
- Learn how Connected Component Analysis (CCA) works.
- Use CCA to produce an image that highlights every object in a different colour.
- Characterise each object with numbers that describe its appearance.
Objects
In the Thresholding episode we have covered dividing an image into foreground and background pixels. In the shapes example image, we considered the coloured shapes as foreground objects on a white background.
In thresholding we went from the original image to this version:
Here, we created a mask that only highlights the parts of the image
that we find interesting, the objects. All objects have pixel
value of True while the background pixels are
False.
By looking at the mask image, one can count the objects that are present in the image (7). But how did we actually do that, how did we decide which lump of pixels constitutes a single object?
Pixel Neighborhoods
In order to decide which pixels belong to the same object, one can exploit their neighborhood: pixels that are directly next to each other and belong to the foreground class can be considered to belong to the same object.
Let’s discuss the concept of pixel neighborhoods in more detail.
Consider the following mask “image” with 8 rows, and 8 columns. For the
purpose of illustration, the digit 0 is used to represent
background pixels, and the letter X is used to represent
object pixels foreground).
OUTPUT
0 0 0 0 0 0 0 0
0 X X 0 0 0 0 0
0 X X 0 0 0 0 0
0 0 0 X X X 0 0
0 0 0 X X X X 0
0 0 0 0 0 0 0 0The pixels are organised in a rectangular grid. In order to
understand pixel neighborhoods we will introduce the concept of “jumps”
between pixels. The jumps follow two rules: First rule is that one jump
is only allowed along the column, or the row. Diagonal jumps are not
allowed. So, from a centre pixel, denoted with o, only the
pixels indicated with a 1 are reachable:
OUTPUT
- 1 -
1 o 1
- 1 -The pixels on the diagonal (from o) are not reachable
with a single jump, which is denoted by the -. The pixels
reachable with a single jump form the 1-jump
neighborhood.
The second rule states that in a sequence of jumps, one may only jump
in row and column direction once -> they have to be
orthogonal. An example of a sequence of orthogonal jumps is
shown below. Starting from o the first jump goes along the
row to the right. The second jump then goes along the column direction
up. After this, the sequence cannot be continued as a jump has already
been made in both row and column direction.
OUTPUT
- - 2
- o 1
- - -All pixels reachable with one, or two jumps form the
2-jump neighborhood. The grid below illustrates the
pixels reachable from the centre pixel o with a single
jump, highlighted with a 1, and the pixels reachable with 2
jumps with a 2.
OUTPUT
2 1 2
1 o 1
2 1 2We want to revisit our example image mask from above and apply the
two different neighborhood rules. With a single jump connectivity for
each pixel, we get two resulting objects, highlighted in the image with
A’s and B’s.
OUTPUT
0 0 0 0 0 0 0 0
0 A A 0 0 0 0 0
0 A A 0 0 0 0 0
0 0 0 B B B 0 0
0 0 0 B B B B 0
0 0 0 0 0 0 0 0In the 1-jump version, only pixels that have direct neighbors along
rows or columns are considered connected. Diagonal connections are not
included in the 1-jump neighborhood. With two jumps, however, we only
get a single object A because pixels are also considered
connected along the diagonals.
OUTPUT
0 0 0 0 0 0 0 0
0 A A 0 0 0 0 0
0 A A 0 0 0 0 0
0 0 0 A A A 0 0
0 0 0 A A A A 0
0 0 0 0 0 0 0 0- 5
- 2
Jumps and neighborhoods
We have just introduced how you can reach different neighboring pixels by performing one or more orthogonal jumps. We have used the terms 1-jump and 2-jump neighborhood. There is also a different way of referring to these neighborhoods: the 4- and 8-neighborhood. With a single jump you can reach four pixels from a given starting pixel. Hence, the 1-jump neighborhood corresponds to the 4-neighborhood. When two orthogonal jumps are allowed, eight pixels can be reached, so the 2-jump neighborhood corresponds to the 8-neighborhood.
Connected Component Analysis
In order to find the objects in an image, we want to employ an
operation that is called Connected Component Analysis (CCA). This
operation takes a binary image as an input. Usually, the
False value in this image is associated with background
pixels, and the True value indicates foreground, or object
pixels. Such an image can be produced, e.g., with thresholding. Given a
thresholded image, the connected component analysis produces a new
labeled image with integer pixel values. Pixels with the same
value, belong to the same object. scikit-image provides connected
component analysis in the function ski.measure.label(). Let
us add this function to the already familiar steps of thresholding an
image.
First, import the packages needed for this episode:
PYTHON
import imageio.v3 as iio
import ipympl
import matplotlib.pyplot as plt
import numpy as np
import skimage as ski
%matplotlib widgetIn this episode, we will use the ski.measure.label
function to perform the CCA.
Next, we define a reusable Python function
connected_components:
PYTHON
def connected_components(filename, sigma=1.0, t=0.5, connectivity=2):
# load the image
image = iio.imread(filename)
# convert the image to grayscale
gray_image = ski.color.rgb2gray(image)
# denoise the image with a Gaussian filter
blurred_image = ski.filters.gaussian(gray_image, sigma=sigma)
# mask the image according to threshold
binary_mask = blurred_image < t
# perform connected component analysis
labeled_image, count = ski.measure.label(binary_mask,
connectivity=connectivity, return_num=True)
return labeled_image, countThe first four lines of code are familiar from the Thresholding episode.
Then we call the ski.measure.label function. This
function has one positional argument where we pass the
binary_mask, i.e., the binary image to work on. With the
optional argument connectivity, we specify the neighborhood
in units of orthogonal jumps. For example, by setting
connectivity=2 we will consider the 2-jump neighborhood
introduced above. The function returns a labeled_image
where each pixel has a unique value corresponding to the object it
belongs to. In addition, we pass the optional parameter
return_num=True to return the maximum label index as
count.
Optional parameters and return values
The optional parameter return_num changes the data type
that is returned by the function ski.measure.label. The
number of labels is only returned if return_num is
True. Otherwise, the function only returns the labeled image.
This means that we have to pay attention when assigning the return value
to a variable. If we omit the optional parameter return_num
or pass return_num=False, we can call the function as
If we pass return_num=True, the function returns a tuple
and we can assign it as
If we used the same assignment as in the first case, the variable
labeled_image would become a tuple, in which
labeled_image[0] is the image and
labeled_image[1] is the number of labels. This could cause
confusion if we assume that labeled_image only contains the
image and pass it to other functions. If you get an
AttributeError: 'tuple' object has no attribute 'shape' or
similar, check if you have assigned the return values consistently with
the optional parameters.
We can call the above function connected_components and
display the labeled image like so:
PYTHON
labeled_image, count = connected_components(filename="data/shapes-01.jpg", sigma=2.0, t=0.9, connectivity=2)
fig, ax = plt.subplots()
ax.imshow(labeled_image)
ax.set_axis_off();If you are using an older version of Matplotlib you might get a
warning
UserWarning: Low image data range; displaying image with stretched contrast.
or just see a visually empty image.
What went wrong? When you hover over the image, the pixel values are
shown as numbers in the lower corner of the viewer. You can see that
some pixels have values different from 0, so they are not
actually all the same value. Let’s find out more by examining
labeled_image. Properties that might be interesting in this
context are dtype, the minimum and maximum value. We can
print them with the following lines:
PYTHON
print("dtype:", labeled_image.dtype)
print("min:", np.min(labeled_image))
print("max:", np.max(labeled_image))Examining the output can give us a clue why the image appears empty.
OUTPUT
dtype: int32
min: 0
max: 11The dtype of labeled_image is
int32. This means that values in this image range from
-2 ** 31 to 2 ** 31 - 1. Those are really big
numbers. From this available space we only use the range from
0 to 11. When showing this image in the
viewer, it may squeeze the complete range into 256 gray values.
Therefore, the range of our numbers does not produce any visible
variation. One way to rectify this is to explicitly specify the data
range we want the colormap to cover:
PYTHON
fig, ax = plt.subplots()
ax.imshow(labeled_image, vmin=np.min(labeled_image), vmax=np.max(labeled_image))Note this is the default behaviour for newer versions of
matplotlib.pyplot.imshow. Alternatively we could convert
the image to RGB and then display it.
Suppressing outputs in Jupyter Notebooks
We just used ax.set_axis_off(); to hide the axis from
the image for a visually cleaner figure. The semicolon is added to
supress the output(s) of the statement, in this case
the axis limits. This is specific to Jupyter Notebooks.
We can use the function ski.color.label2rgb() to convert
the 32-bit grayscale labeled image to standard RGB colour (recall that
we already used the ski.color.rgb2gray() function to
convert to grayscale). With ski.color.label2rgb(), all
objects are coloured according to a list of colours that can be
customised. We can use the following commands to convert and show the
image:
PYTHON
# convert the label image to color image
colored_label_image = ski.color.label2rgb(labeled_image, bg_label=0)
fig, ax = plt.subplots()
ax.imshow(colored_label_image)
ax.set_axis_off();
How many objects are in that image (15 min)
Now, it is your turn to practice. Using the function
connected_components, find two ways of printing out the
number of objects found in the image.
What number of objects would you expect to get?
How does changing the sigma and threshold
values influence the result?
As you might have guessed, the return value count
already contains the number of objects found in the image. So it can
simply be printed with
But there is also a way to obtain the number of found objects from
the labeled image itself. Recall that all pixels that belong to a single
object are assigned the same integer value. The connected component
algorithm produces consecutive numbers. The background gets the value
0, the first object gets the value 1, the
second object the value 2, and so on. This means that by
finding the object with the maximum value, we also know how many objects
there are in the image. We can thus use the np.max function
from NumPy to find the maximum value that equals the number of found
objects:
Invoking the function with sigma=2.0, and
threshold=0.9, both methods will print
OUTPUT
Found 11 objects in the image.Lowering the threshold will result in fewer objects. The higher the threshold is set, the more objects are found. More and more background noise gets picked up as objects. Larger sigmas produce binary masks with less noise and hence a smaller number of objects. Setting sigma too high bears the danger of merging objects.
You might wonder why the connected component analysis with
sigma=2.0, and threshold=0.9 finds 11 objects,
whereas we would expect only 7 objects. Where are the four additional
objects? With a bit of detective work, we can spot some small objects in
the image, for example, near the left border.
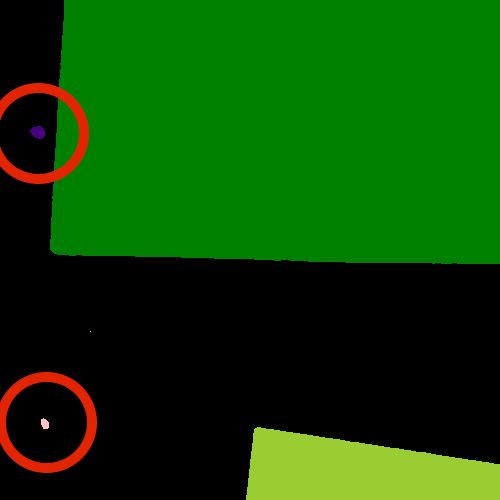
For us it is clear that these small spots are artifacts and not
objects we are interested in. But how can we tell the computer? One way
to calibrate the algorithm is to adjust the parameters for blurring
(sigma) and thresholding (t), but you may have
noticed during the above exercise that it is quite hard to find a
combination that produces the right output number. In some cases,
background noise gets picked up as an object. And with other parameters,
some of the foreground objects get broken up or disappear completely.
Therefore, we need other criteria to describe desired properties of the
objects that are found.
Morphometrics - Describe object features with numbers
Morphometrics is concerned with the quantitative analysis of objects
and considers properties such as size and shape. For the example of the
images with the shapes, our intuition tells us that the objects should
be of a certain size or area. So we could use a minimum area as a
criterion for when an object should be detected. To apply such a
criterion, we need a way to calculate the area of objects found by
connected components. Recall how we determined the root mass in the Thresholding episode by
counting the pixels in the binary mask. But here we want to calculate
the area of several objects in the labeled image. The scikit-image
library provides the function ski.measure.regionprops to
measure the properties of labeled regions. It returns a list of
RegionProperties that describe each connected region in the
images. The properties can be accessed using the attributes of the
RegionProperties data type. Here we will use the properties
"area" and "label". You can explore the
scikit-image documentation to learn about other properties
available.
We can get a list of areas of the labeled objects as follows:
PYTHON
# compute object features and extract object areas
object_features = ski.measure.regionprops(labeled_image)
object_areas = [objf["area"] for objf in object_features]
object_areasThis will produce the output
OUTPUT
[318542, 1, 523204, 496613, 517331, 143, 256215, 1, 68, 338784, 265755]Plot a histogram of the object area distribution (10 min)
Similar to how we determined a “good” threshold in the Thresholding episode, it is often helpful to inspect the histogram of an object property. For example, we want to look at the distribution of the object areas.
- Create and examine a histogram of the object areas
obtained with
ski.measure.regionprops. - What does the histogram tell you about the objects?
The histogram can be plotted with
PYTHON
fig, ax = plt.subplots()
ax.hist(object_areas)
ax.set_xlabel("Area (pixels)")
ax.set_ylabel("Number of objects");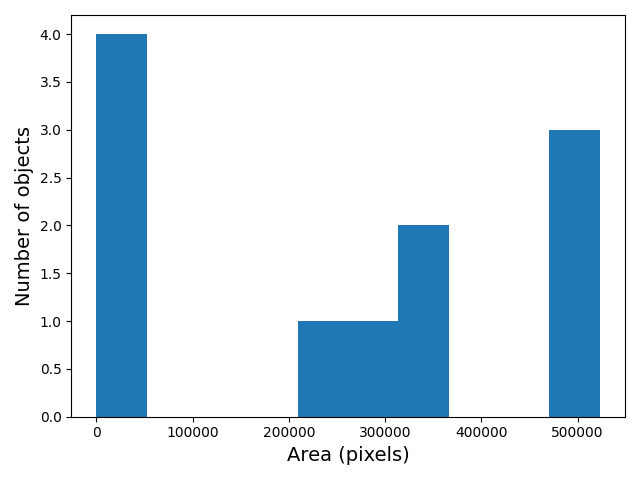
The histogram shows the number of objects (vertical axis) whose area is within a certain range (horizontal axis). The height of the bars in the histogram indicates the prevalence of objects with a certain area. The whole histogram tells us about the distribution of object sizes in the image. It is often possible to identify gaps between groups of bars (or peaks if we draw the histogram as a continuous curve) that tell us about certain groups in the image.
In this example, we can see that there are four small objects that
contain less than 50000 pixels. Then there is a group of four (1+1+2)
objects in the range between 200000 and 400000, and three objects with a
size around 500000. For our object count, we might want to disregard the
small objects as artifacts, i.e, we want to ignore the leftmost bar of
the histogram. We could use a threshold of 50000 as the minimum area to
count. In fact, the object_areas list already tells us that
there are fewer than 200 pixels in these objects. Therefore, it is
reasonable to require a minimum area of at least 200 pixels for a
detected object. In practice, finding the “right” threshold can be
tricky and usually involves an educated guess based on domain
knowledge.
One way to count only objects above a certain area is to first create a list of those objects, and then take the length of that list as the object count. This can be done as follows:
PYTHON
min_area = 200
large_objects = []
for objf in object_features:
if objf["area"] > min_area:
large_objects.append(objf["label"])
print("Found", len(large_objects), "objects!")Another option is to use NumPy arrays to create the list of large
objects. We first create an array object_areas containing
the object areas, and an array object_labels containing the
object labels. The labels of the objects are also returned by
ski.measure.regionprops. We have already seen that we can
create boolean arrays using comparison operators. Here we can use
object_areas > min_area to produce an array that has the
same dimension as object_labels. It can then used to select
the labels of objects whose area is greater than min_area
by indexing:
PYTHON
object_areas = np.array([objf["area"] for objf in object_features])
object_labels = np.array([objf["label"] for objf in object_features])
large_objects = object_labels[object_areas > min_area]
print("Found", len(large_objects), "objects!")The advantage of using NumPy arrays is that for loops
and if statements in Python can be slow, and in practice
the first approach may not be feasible if the image contains a large
number of objects. In that case, NumPy array functions turn out to be
very useful because they are much faster.
In this example, we can also use the np.count_nonzero
function that we have seen earlier together with the >
operator to count the objects whose area is above
min_area.
For all three alternatives, the output is the same and gives the expected count of 7 objects.
To remove the small objects from the labeled image, we change the value of all pixels that belong to the small objects to the background label 0. One way to do this is to loop over all objects and set the pixels that match the label of the object to 0.
PYTHON
for object_id, objf in enumerate(object_features, start=1):
if objf["area"] < min_area:
labeled_image[labeled_image == objf["label"]] = 0Here NumPy functions can also be used to eliminate for
loops and if statements. Like above, we can create an array
of the small object labels with the comparison
object_areas < min_area. We can use another NumPy
function, np.isin, to set the pixels of all small objects
to 0. np.isin takes two arrays and returns a boolean array
with values True if the entry of the first array is found
in the second array, and False otherwise. This array can
then be used to index the labeled_image and set the entries
that belong to small objects to 0.
PYTHON
object_areas = np.array([objf["area"] for objf in object_features])
object_labels = np.array([objf["label"] for objf in object_features])
small_objects = object_labels[object_areas < min_area]
labeled_image[np.isin(labeled_image, small_objects)] = 0An even more elegant way to remove small objects from the image is to
leverage the ski.morphology module. It provides a function
ski.morphology.remove_small_objects that does exactly what
we are looking for. It can be applied to a binary image and returns a
mask in which all objects smaller than min_area are
excluded, i.e, their pixel values are set to False. We can
then apply ski.measure.label to the masked image:
PYTHON
object_mask = ski.morphology.remove_small_objects(binary_mask, min_size=min_area)
labeled_image, n = ski.measure.label(object_mask,
connectivity=connectivity, return_num=True)Using the scikit-image features, we can implement the
enhanced_connected_component as follows:
PYTHON
def enhanced_connected_components(filename, sigma=1.0, t=0.5, connectivity=2, min_area=0):
image = iio.imread(filename)
gray_image = ski.color.rgb2gray(image)
blurred_image = ski.filters.gaussian(gray_image, sigma=sigma)
binary_mask = blurred_image < t
object_mask = ski.morphology.remove_small_objects(binary_mask, min_size=min_area)
labeled_image, count = ski.measure.label(object_mask,
connectivity=connectivity, return_num=True)
return labeled_image, countWe can now call the function with a chosen min_area and
display the resulting labeled image:
PYTHON
labeled_image, count = enhanced_connected_components(filename="data/shapes-01.jpg", sigma=2.0, t=0.9,
connectivity=2, min_area=min_area)
colored_label_image = ski.color.label2rgb(labeled_image, bg_label=0)
fig, ax = plt.subplots()
ax.imshow(colored_label_image)
ax.set_axis_off();
print("Found", count, "objects in the image.")
OUTPUT
Found 7 objects in the image.Note that the small objects are “gone” and we obtain the correct number of 7 objects in the image.
We already know how to get the areas of the objects from the
regionprops. We just need to insert a zero area value for
the background (to colour it like a zero size object). The background is
also labeled 0 in the labeled_image, so we
insert the zero area value in front of the first element of
object_areas with np.insert. Then we can
create a colored_area_image where we assign each pixel
value the area by indexing the object_areas with the label
values in labeled_image.
PYTHON
object_areas = np.array([objf["area"] for objf in ski.measure.regionprops(labeled_image)])
# prepend zero to object_areas array for background pixels
object_areas = np.insert(0, obj=1, values=object_areas)
# create image where the pixels in each object are equal to that object's area
colored_area_image = object_areas[labeled_image]
fig, ax = plt.subplots()
im = ax.imshow(colored_area_image)
cbar = fig.colorbar(im, ax=ax, shrink=0.85)
cbar.ax.set_title("Area")
ax.set_axis_off();
Callout
You may have noticed that in the solution, we have used the
labeled_image to index the array object_areas.
This is an example of advanced
indexing in NumPy The result is an array of the same shape as the
labeled_image whose pixel values are selected from
object_areas according to the object label. Hence the
objects will be colored by area when the result is displayed. Note that
advanced indexing with an integer array works slightly different than
the indexing with a Boolean array that we have used for masking. While
Boolean array indexing returns only the entries corresponding to the
True values of the index, integer array indexing returns an
array with the same shape as the index. You can read more about advanced
indexing in the NumPy
documentation.
Key Points
- We can use
ski.measure.labelto find and label connected objects in an image. - We can use
ski.measure.regionpropsto measure properties of labeled objects. - We can use
ski.morphology.remove_small_objectsto mask small objects and remove artifacts from an image. - We can display the labeled image to view the objects coloured by label.